Newton-Raphson’s method, commonly known as
NR method is one of the most widely used and fast methods for solving
equations.
This method is also based on the
linear approximation of the function but does so using a tangent to the curve.
Starting from a single initial estimate, x0 that is not too far
from the root, we move along the tangent to its intersection with the x-axis,
and take that as the next approximation. This is continued until either the
successive x-values are sufficiently close or the value of the function is
sufficiently close to zero.
This algorithm is widely used because, at
least in the near neighborhood of a root, it is more rapidly convergent than
any of the methods. The net result of this is that the number of decimal places
of accuracy nearly doubles at each iteration. However, there is the need of two
functions evaluation at each steps, f(x) and f’(x). If at any approximation
point, the f ’(x) is zero, then the solution cannot be achieved and due to low
value of f’(x) at any step, the root may be diverge away from the required one.
From above figures we have,
where f(x) is continuous and f
’(x) ≠ 0.
Newton-Raphson’s method, commonly known as
NR method is one of the most widely used and fast methods for solving
equations.
This method is also based on the
linear approximation of the function but does so using a tangent to the curve.
Starting from a single initial estimate, x0 that is not too far
from the root, we move along the tangent to its intersection with the x-axis,
and take that as the next approximation. This is continued until either the
successive x-values are sufficiently close or the value of the function is
sufficiently close to zero.
This algorithm is widely used because, at
least in the near neighborhood of a root, it is more rapidly convergent than
any of the methods. The net result of this is that the number of decimal places
of accuracy nearly doubles at each iteration. However, there is the need of two
functions evaluation at each steps, f(x) and f’(x). If at any approximation
point, the f ’(x) is zero, then the solution cannot be achieved and due to low
value of f’(x) at any step, the root may be diverge away from the required one.
From above figures we have,
Slope of tangent = f’(x) = f(x0)/(x0-x1)
i.e x1 = x0 – f’(x0)/f(x0)
i.e xn+1 = xn – f’(xn)/f(xn)
where f(x) is continuous and f
’(x) ≠ 0.
Source
Code in C Programming
}while(fabs(err)>0.00001);
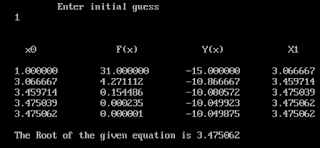
In above code we have taken
equation as x*x-17*x+47 so its possible solution are :
3.47 and 13.52 .
And its derivative is 2*x-17.
So when we guess the value 1
i.e it is close to root 3.47 so root is 3.47 similarly if we guess 9 i.e close
to 13 so it converges to 13.52.
Every iteration can be
displayed by insertion some addition lines: line ** and line
*** (in below code) as shown in below:
#include<stdio.h>
#include<math.h>
#include<conio.h>
#define f(x) x*x-17*x+47
#define y(x) 2*x-17
void main()
{
clrscr();
float
x,x1,fa,fb,err;
printf("\n\t\tEnter initial guess\t\n\t");
scanf("%f",&x);
//line **
printf("\n\n\t
x0\t\t F(x)\t\t Y(x)\t\t X1\n\n");
do{
fa=f(x);
fb=y(x);
x1=x-(fa/fb);
//line ***
printf("\t%f\t%f\t%f\t%f\t\n",x,fa,fb,x1);
err=(x1-x);
x=x1;
}while(fabs(err)>0.00001);
printf("\n\tThe Root of the given
equation is %f\n",x);
getch();
}
Sample run
NOTE: The number of
iteration reduces as the guess is closed to the root. In above when guess is 1
the total iteration is only 5 since 1 is very close to root 3.47 but when
guess is 9 it takes 8 iteration sine 9 is a bit far from root 13.52.



No comments:
Post a Comment