SECANT METHOD

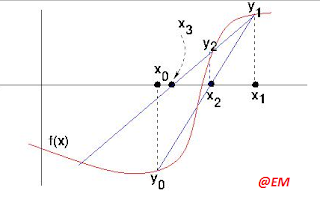
The Secant method begins by finding two points on the curve of f(x) hopefully near to the root we seek. A graph or few applications of bisection method might be used to determine the approximate of the root. We draw the line through these two points and find where it intersects the x-axis. The two points may both be on one side of the root or on opposite sides.         

          If f(x) were truly linear, the straight line would intersect the x-axis at the root. Because f(x) will never be linear as we do not use root finding method for linear function, the intersection point is not equal to root, but it should be closer than either of the two points we began with.

 PROGRAM  CODE  IN  C  Programming

#include<stdio.h>

#include<math.h>

#include<conio.h>

#define f(x)  x*x-17*x+47

#define err 0.0001

void main()

{   clrscr();

    float a,b,x;

    float fa,fb,fx;

    printf("\n\tEnter two initial guesses\n\t");

    scanf("%f%f",&a,&b);

   

    do{

              fa=f(a);

              fb=f(b);

              x=((a*fb)-(b*fa))/(fb-fa);

              fx=f(x);

              a=b;

              b=x;

}while(fabs(a-b)>err);

          printf("\tRoot is %f\n",x);

          getch();

}

Sample Run

In this program we have taken the reference equation as:   x²-17x+47 = 0 so the roots are 3.47 and 13.53 respectively.

So if we guess the root near 3.47 then the output is 3.47 and similarly if our guess is near the root 13.53 then the output is 13.57 which are shown below respectively: 

Also all the iteration can be shown by adding few lines of codes as shown in below:

(Here lines ln @ and ln @@ is added.)

#include<stdio.h>

#include<math.h>

#include<conio.h>

#define f(x)  x*x-17*x+47

#define err 0.0001

void main()

{   clrscr();

    float a,b,x;

    float fa,fb,fx;

    printf("\n\tEnter two initial guesses\n\t");

    scanf("%f%f",&a,&b);

//ln @:  

 printf("\n\t  A\t      B\t        F(A)\t    F(B)\t  X\t    F(X)\n\n");

    do{

              fa=f(a);

              fb=f(b);

              x=((a*fb)-(b*fa))/(fb-fa);

//ln @@

          printf("\t%f   %f   %f   %f   %f   %f\n\n",a,b,fa,fb,x,fx);

              fx=f(x);

              a=b;

              b=x;

}while(fabs(a-b)>err);

          printf("\tRoot is %f\n",x);

          getch();

}

Sample Run

If we guess the root near 3.47 then the output is 3.47 and similarly if our guess is near the root 13.53 then the output is 13.57  but all the iteration can be shown as below: