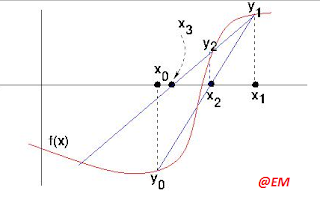
The Secant method begins
by finding two points on the curve of f(x) hopefully near to the root we seek.
A graph or few applications of bisection method might be used to determine the
approximate of the root. We draw the line through these two points and find
where it intersects the x-axis. The two points may both be on one side of the
root or on opposite
sides.
If f(x) were truly linear, the straight line
would intersect the x-axis at the root. Because f(x) will never be linear as we
do not use root finding method for linear function, the intersection point is
not equal to root, but it should be closer than either of the two points we
began with.
PROGRAM CODE IN C Programming
#include<stdio.h>
#include<math.h>
#include<conio.h>
#define f(x) x*x-17*x+47
#define err 0.0001
void main()
{ clrscr();
float a,b,x;
float fa,fb,fx;
printf("\n\tEnter two initial
guesses\n\t");
scanf("%f%f",&a,&b);
do{
fa=f(a);
fb=f(b);
x=((a*fb)-(b*fa))/(fb-fa);
fx=f(x);
a=b;
b=x;
}while(fabs(a-b)>err);
printf("\tRoot is %f\n",x);
getch();
}
Sample Run
In this program we have
taken the reference equation as: x2-17x+47 = 0 so the roots are 3.47
and 13.53 respectively.
So if we guess the root
near 3.47 then the output is 3.47 and similarly if our guess is near the root
13.53 then the output is 13.57 which are shown below respectively:
Also all the iteration
can be shown by adding few lines of codes as shown in below:
(Here lines ln @ and ln
@@ is added.)
#include<stdio.h>
#include<math.h>
#include<conio.h>
#define f(x) x*x-17*x+47
#define err 0.0001
void main()
{ clrscr();
float a,b,x;
float fa,fb,fx;
printf("\n\tEnter two initial
guesses\n\t");
scanf("%f%f",&a,&b);
//ln @:
printf("\n\t A\t B\t F(A)\t F(B)\t X\t F(X)\n\n");
do{
fa=f(a);
fb=f(b);
x=((a*fb)-(b*fa))/(fb-fa);
//ln @@
printf("\t%f %f %f %f %f %f\n\n",a,b,fa,fb,x,fx);
fx=f(x);
a=b;
b=x;
}while(fabs(a-b)>err);
printf("\tRoot is %f\n",x);
getch();
}




good informaton
ReplyDeleteThanks for you feedback
Delete