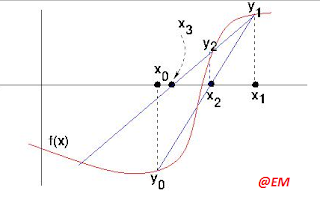
GAUSS SEIDAL METHOD

             Gauss Seidel method is one of the iterative methods to solve the simultaneous algebraic equations. It is the most easy and fastest method among all other iterative method to solve the simultaneous algebraic equations.

Program code for Gauss Seidel method

Below is the Program code for Gauss Seidel method written in C programming using code blocks libraries.

#include<stdio.h>

#include<math.h>

#define e 0.000001

int main()

{

    float a[20][20];

    int i,j,n;

    float sum=0;

    float x[20],y[20],error[20],errormax;

    printf("enter no of equation:");

    scanf("%d",&n);

    printf("Enter the augumented matrix:");

    for(i=1;i<=n;i++)

    {

        for(j=1;j<=n+1;j++)

        {

            printf("a[%d][%d]=",i,j);

            scanf("%f",&a[i][j]);

        }

    }

    for(i=1;i<=n;i++)

    {

        x[i]=a[i][n+1]/a[i][i];

    }

    do

    {

     for(i=1;i<=n;i++)

     {

         sum=0;

         for(j=1;j<=n;j++)

         {

             if(i!=j)

                 sum=sum+a[i][j]*x[j];

         }

         y[i]=(a[i][n+1]-sum)/a[i][i];

         error[i]=fabs(y[i]-x[i]);

         x[i]=y[i];

     }

     errormax=error[1]; // maxm error among error vector

     for(i=2;i<=n;i++)

     {

         if(errormax<error[i])

            errormax=error[i];

     }

    }while(fabs(errormax)>e);

    for(i=1;i<=n;i++)

    {

       printf("result is %f",x[i]);

    }

return 0;

}

GAUSS JORDAN -- INVERSE METHOD

                    
                Gauss Jordan Inverse method is one of the procedure to find the inverse of a given matrix.

The steps involved in this method is almost same as the Gauss Jordan method to solve the simulation algebraic equations but it has some extra steps. The program codes given below helps to find the inverse using Gauss Jordan method.

Program code for Gauss Jordan – Inverse Method

#include<iostream>

#include<cmath>

#include<cstdlib>

using namespace std;

void display(float array[][30], int size){

    for(int i = 0; i < size; i++){

        for (int j = 0; j<2*size; j++)

            cout<<array[i][j]<<"\t";

        cout<<endl<<endl;

    }

}

int main(){

    int size;

    float array[30][30], temp;

    cout<<"Enter the number of variables : ";

    cin>>size;

    for(int i = 0; i < size; i++){

        for (int j = 0; j<size; j++)

            cin>>array[i][j];

    }

    for (int i= 0; i<size; i++){

        for (int j = size; j<2*size; j++){

            if( (i + size) == j)

                array[i][j] = 1;

            else array[i][j] = 0;

        }

    }

    cout<<"Provided Matrix :"<<endl;

    display(array, size);

    for (int j = 0; j < size; j++){

        for (int i = 0; i < size; i++){

            if (i != j){

                temp = array[i][j]/array[j][j];

                for (int k = 0; k < 2*size; k++){

                        array[i][k] = array[i][k] - (temp*array[j][k]);

                }

            }

        }

    }

    cout<<"Final Matrix :"<<endl;

    display(array, size);

    for (int i = 0; i < size; i++){

        float temp = array[i][i];

        for (int j = 0; j< (2*size); j++){

            array[i][j] = array[i][j]/temp;

        }

    }

    cout<<"Inverse Matrix :"<<endl;

    display(array, size);

    float inverse[30][30];

    for (int i = 0; i<size; i++){

        for (int j = size; j< 2*size; j++)

            inverse[i][j-size] = array[i][j];

    }

    cout<<"Final Inveerse Matrix :"<<endl;

    for(int i = 0; i < size; i++){

        for (int j = 0; j<size; j++)

            cout<<inverse[i][j]<<"\t";

        cout<<endl<<endl;

    }

    return 0;

}

(Note: Above source code is written using C++ programming in code block)

GAUSS JORDAN METHOD

            Gauss Jordan method is the modification Gauss Elimination method hence it is also one of the procedures to solve the simultaneous algebraic equation.

          In this method, elimination of unknown is performed not in the equation below but in the equation above also, reducing the system to a diagonal matrix form i.e. each equation involving only one unknown. From these equations the unknowns can be obtained readily.

          Thus in this method, the labor of back substitution for finding the unknowns is saved at the cost of addition calculation.

Source Code

#include<stdio.h>

#include<conio.h>

#include<math.h>

void main()

{

    int i,n,j,k;

    float pivot,f,x[10],sum=0;

    float a[10][10];

    printf("\n\n\t\tEnter the no of equations::\n\t");

    scanf("%d",&n);

    printf("\n\t\tEnter the matrix:\n");

    for(i=1;i<=n;i++)

    {

        for(j=1;j<=n+1;j++)

        {

            printf("\t\ta[%d][%d]=",i,j);

            scanf("%f",&a[i][j]);

        }

        printf("\n\n");

    }

    for(k=1;k<=n-1;k++)

    {

        pivot=a[k][k];

        for(i=k+1;i<=n;i++)

        {

            f=a[i][k]/pivot;

            for(j=k;j<=(n+1);j++)

            {

                a[i][j]=a[i][j]-f*a[k][j];

            }

        }

    }

    for(k=n;k>=2;k--)

    {

        pivot=a[k][k];

        for(i=k-1;i>=1;i--)

        {

            f=a[i][k]/pivot;

            for(j=k;j<=(n+1);j++)

            {

                a[i][j]=a[i][j]-f*a[k][j];

            }

        }

    }

    printf("\n\n\t\t The diagnol matrix is:\n\n");

    for(i=1;i<=n;i++)

    {

        for(j=1;j<=(n+1);j++)

        {

            printf("\t%f",a[i][j]);

        }

        printf("\n");

    }

    for(i=1;i<=n;i++)

    {

        x[i]=(a[i][n+1])/a[i][i];

    }

    printf("\n\tThe value is:\n\n");

    for(i=1;i<=n;i++)

    {

       printf("\tx%d=%f\t",i,x[i]);

    }

    getch();

}

Sample output:

In this output only two equations is taken for references. Any number of equations can be taken.

The output of Gauss Jordan method is shown as:

( Note: Above source code is written using C programming in TurboC++)

GAUSS ELIMINATION METHOD

         Gauss Elimination method is one of the procedures to solve the simultaneous algebraic equation.

          In this method, the unknowns are eliminated successively and the system is reduced to an upper triangular system from which the unknown are found by back substitution. The method is quite general and is well adapted for computer operations.

Program Code

#include<stdio.h>

#include<conio.h>

#include<math.h>

void main()

{

    int i,n,j,k;

    float pivot,f,x[10],sum=0;

    float a[10][10];

    printf("\n\n\t\tEnter the no of eqns\n\t\t");

    scanf("%d",&n);

    printf("\n\t\tEnter the matrix:\n");

    for(i=1;i<=n;i++)

    {

        for(j=1;j<=n+1;j++)

        {

            printf("\t\ta[%d][%d]=",i,j);

            scanf("%f",&a[i][j]);

        }

    }

    for(k=1;k<=n-1;k++)

    {

        pivot=a[k][k];

        for(i=k+1;i<=n;i++)

        {

            f=a[i][k]/pivot;

            for(j=k;j<=(n+1);j++)

            {

                a[i][j]=a[i][j]-f*a[k][j];

            }

        }

    }

    printf("\tMatrix in echelon form:\n\n");

    for(i=1;i<=n;i++)

    {

        for(j=1;j<=(n+1);j++)

        {

            printf("\t%f",a[i][j]);

        }

        printf("\n");

    }

    x[n]=(a[n][n+1])/a[n][n];

    for(i=n-1;i>=1;i--)

    {

        sum=0;

        for(j=i+1;j<=n;j++)

        {

            sum=sum+a[i][j]*x[j];

        }

        x[i]=(a[i][n+1]-sum)/a[i][i];

    }

    printf("\n\tThe solution is:\n");

    for(i=1;i<=n;i++)

    {

       printf("\n\tx%d  =  %f\t",i,x[i]);

    }

    getch();

}

Sample output:

In this output only two equations is taken for references. Any number of equations can be taken.

The output of Gauss Elimination method is shown as:

Note: This code is implemented in C programming using TurboC++ libraries.

FIXED POINT ITERATION

Fixed point iteration is one of the methods to calculate the root of the equation. It is also based on the numbers of iteration.

 In this method given equation f(x) = 0 is first converted into x=g(x),

 then using iterative recursive formula others values are calculated as:

 x_i+1 = g(x_i)  where i=0,1,2,3,…..

and x₀  is guessed initially.

Program Code Implemented in C++

#include<iomanip>

#include<iostream>

#include<math.h>

#define e 0.00001

using namespace std;

float g(float a)

{

          return(0.5*((1/(a*a+a))+a));

}

int main()

{

          float x1,x2,x3;

          int i=1;

          cout<<"The given function is f(X)=x^3+X^2-1"<<endl;

    cout<<"Enter your initial guess:";

    cin>>x1;

          cout<<setw(2)<<"No."<<setw(12)<<"x1"<<setw(30)<<"x2=0.5((1/(X^2+X))+X)"<<setw(14)<<"Upgrade"<<endl;

          do

          {

              x2=g(x1);

                   cout<<setw(2)<<i<<setw(13)<<x1<<setw(30)<<x2<<setw(14)<<"x1=x2"<<endl;

                   i++;

                    x3=x1;

                   x1=x2;

    }while( fabs(x1-x3) >= e);

          cout<<"\nTHE REQUIRED Root IS ="<<x2;

          return 0;

}

NOTE: The above code is implemented in c++ and written using code blocks libraries.

SECANT METHOD

The Secant method begins by finding two points on the curve of f(x) hopefully near to the root we seek. A graph or few applications of bisection method might be used to determine the approximate of the root. We draw the line through these two points and find where it intersects the x-axis. The two points may both be on one side of the root or on opposite sides.         

          If f(x) were truly linear, the straight line would intersect the x-axis at the root. Because f(x) will never be linear as we do not use root finding method for linear function, the intersection point is not equal to root, but it should be closer than either of the two points we began with.

 PROGRAM  CODE  IN  C  Programming

#include<stdio.h>

#include<math.h>

#include<conio.h>

#define f(x)  x*x-17*x+47

#define err 0.0001

void main()

{   clrscr();

    float a,b,x;

    float fa,fb,fx;

    printf("\n\tEnter two initial guesses\n\t");

    scanf("%f%f",&a,&b);

   

    do{

              fa=f(a);

              fb=f(b);

              x=((a*fb)-(b*fa))/(fb-fa);

              fx=f(x);

              a=b;

              b=x;

}while(fabs(a-b)>err);

          printf("\tRoot is %f\n",x);

          getch();

}

Sample Run

In this program we have taken the reference equation as:   x²-17x+47 = 0 so the roots are 3.47 and 13.53 respectively.

So if we guess the root near 3.47 then the output is 3.47 and similarly if our guess is near the root 13.53 then the output is 13.57 which are shown below respectively: 

Also all the iteration can be shown by adding few lines of codes as shown in below:

(Here lines ln @ and ln @@ is added.)

#include<stdio.h>

#include<math.h>

#include<conio.h>

#define f(x)  x*x-17*x+47

#define err 0.0001

void main()

{   clrscr();

    float a,b,x;

    float fa,fb,fx;

    printf("\n\tEnter two initial guesses\n\t");

    scanf("%f%f",&a,&b);

//ln @:  

 printf("\n\t  A\t      B\t        F(A)\t    F(B)\t  X\t    F(X)\n\n");

    do{

              fa=f(a);

              fb=f(b);

              x=((a*fb)-(b*fa))/(fb-fa);

//ln @@

          printf("\t%f   %f   %f   %f   %f   %f\n\n",a,b,fa,fb,x,fx);

              fx=f(x);

              a=b;

              b=x;

}while(fabs(a-b)>err);

          printf("\tRoot is %f\n",x);

          getch();

}

Sample Run

If we guess the root near 3.47 then the output is 3.47 and similarly if our guess is near the root 13.53 then the output is 13.57  but all the iteration can be shown as below: